1. The Nature of Econometrics and Economic Data

Datasets can be accessed from Boston College

import pandas as pd
from wooldridge import *
dataWoo()

  J.M. Wooldridge (2016) Introductory Econometrics: A Modern Approach,
  Cengage Learning, 6th edition.

  401k       401ksubs    admnrev       affairs     airfare
  alcohol    apple       approval      athlet1     athlet2
  attend     audit       barium        beauty      benefits
  beveridge  big9salary  bwght         bwght2      campus
  card       catholic    cement        census2000  ceosal1
  ceosal2    charity     consump       corn        countymurders
  cps78_85   cps91       crime1        crime2      crime3
  crime4     discrim     driving       earns       econmath
  elem94_95  engin       expendshares  ezanders    ezunem
  fair       fertil1     fertil2       fertil3     fish
  fringe     gpa1        gpa2          gpa3        happiness
  hprice1    hprice2     hprice3       hseinv      htv
  infmrt     injury      intdef        intqrt      inven
  jtrain     jtrain2     jtrain3       kielmc      lawsch85
  loanapp    lowbrth     mathpnl       meap00_01   meap01
  meap93     meapsingle  minwage       mlb1        mroz
  murder     nbasal      nyse          okun        openness
  pension    phillips    pntsprd       prison      prminwge
  rdchem     rdtelec     recid         rental      return
  saving     sleep75     slp75_81      smoke       traffic1
  traffic2   twoyear     volat         vote1       vote2
  voucher    wage1       wage2         wagepan     wageprc
  wine

Exercises

C1

Use the data in WAGE1 for this exercise.

df = dataWoo('WAGE1')
dataWoo('Wage1', description=True)

name of dataset: wage1
no of variables: 24
no of observations: 526

+----------+---------------------------------+
| variable | label                           |
+----------+---------------------------------+
| wage     | average hourly earnings         |
| educ     | years of education              |
| exper    | years potential experience      |
| tenure   | years with current employer     |
| nonwhite | =1 if nonwhite                  |
| female   | =1 if female                    |
| married  | =1 if married                   |
| numdep   | number of dependents            |
| smsa     | =1 if live in SMSA              |
| northcen | =1 if live in north central U.S |
| south    | =1 if live in southern region   |
| west     | =1 if live in western region    |
| construc | =1 if work in construc. indus.  |
| ndurman  | =1 if in nondur. manuf. indus.  |
| trcommpu | =1 if in trans, commun, pub ut  |
| trade    | =1 if in wholesale or retail    |
| services | =1 if in services indus.        |
| profserv | =1 if in prof. serv. indus.     |
| profocc  | =1 if in profess. occupation    |
| clerocc  | =1 if in clerical occupation    |
| servocc  | =1 if in service occupation     |
| lwage    | log(wage)                       |
| expersq  | exper^2                         |
| tenursq  | tenure^2                        |
+----------+---------------------------------+

These are data from the 1976 Current Population Survey, collected by
Henry Farber when he and I were colleagues at MIT in 1988.

df.head()

	wage	educ	exper	tenure	nonwhite	female	married	numdep	smsa	northcen	...	trcommpu	trade	services	profserv	profocc	clerocc	servocc	lwage	expersq	tenursq
0	3.10	11	2	0	0	1	0	2	1	0	...	0	0	0	0	0	0	0	1.131402	4	0
1	3.24	12	22	2	0	1	1	3	1	0	...	0	0	1	0	0	0	1	1.175573	484	4
2	3.00	11	2	0	0	0	0	2	0	0	...	0	1	0	0	0	0	0	1.098612	4	0
3	6.00	8	44	28	0	0	1	0	1	0	...	0	0	0	0	0	1	0	1.791759	1936	784
4	5.30	12	7	2	0	0	1	1	0	0	...	0	0	0	0	0	0	0	1.667707	49	4

5 rows × 24 columns

(i) Find the average education level in the sample. What are the lowest and highest years of education?

print("Average edu years:", df["educ"].mean().__round__(1))

print("Lowest edu years:", df["educ"].min())

print("Highest edu years:", df["educ"].max())

Average edu years: 12.6
Lowest edu years: 0
Highest edu years: 18

(ii) Find the average hourly wage in the sample. Does it seem high or low?

print("Average hourly wage:", df["wage"].mean().__round__(1))

Average hourly wage: 5.9

(v) How many women are in the sample? How many men?

print("Number of females:", df["female"].value_counts().sort_values().iloc[0])

print("Number of males:", df["female"].value_counts().sort_values().iloc[1])

Number of females: 252
Number of males: 274

C2

Use the data in BWGHT to answer this question

df2 = dataWoo('BWGHT')
dataWoo('BWGHT', description=True)

name of dataset: bwght
no of variables: 14
no of observations: 1388

+----------+--------------------------------+
| variable | label                          |
+----------+--------------------------------+
| faminc   | 1988 family income, $1000s     |
| cigtax   | cig. tax in home state, 1988   |
| cigprice | cig. price in home state, 1988 |
| bwght    | birth weight, ounces           |
| fatheduc | father's yrs of educ           |
| motheduc | mother's yrs of educ           |
| parity   | birth order of child           |
| male     | =1 if male child               |
| white    | =1 if white                    |
| cigs     | cigs smked per day while preg  |
| lbwght   | log of bwght                   |
| bwghtlbs | birth weight, pounds           |
| packs    | packs smked per day while preg |
| lfaminc  | log(faminc)                    |
+----------+--------------------------------+

J. Mullahy (1997), “Instrumental-Variable Estimation of Count Data
Models: Applications to Models of Cigarette Smoking Behavior,” Review
of Economics and Statistics 79, 596-593. Professor Mullahy kindly
provided the data. He obtained them from the 1988 National Health
Interview Survey.

df2.head()

	faminc	cigtax	cigprice	bwght	fatheduc	motheduc	parity	male	white	cigs	lbwght	bwghtlbs	packs	lfaminc
0	13.5	16.5	122.300003	109	12.0	12.0	1	1	1	0	4.691348	6.8125	0.0	2.602690
1	7.5	16.5	122.300003	133	6.0	12.0	2	1	0	0	4.890349	8.3125	0.0	2.014903
2	0.5	16.5	122.300003	129	NaN	12.0	2	0	0	0	4.859812	8.0625	0.0	-0.693147
3	15.5	16.5	122.300003	126	12.0	12.0	2	1	0	0	4.836282	7.8750	0.0	2.740840
4	27.5	16.5	122.300003	134	14.0	12.0	2	1	1	0	4.897840	8.3750	0.0	3.314186

(i) How many women are in the sample, and how many report smoking during pregnancy?

print("Numbers of females:", df2.shape[0])

print("Smoking during pregnancy:",
      (df2[df2['cigs'] != 0]).shape[0])

Numbers of females: 1388
Smoking during pregnancy: 212

(ii) What is the average number of cigarettes smoked per day? Is the average a good measure of the “typical” woman in this case? Explain

print("Mean cigs:", df2['cigs'].mean().__round__(1))

print('Median cigs:', df2['cigs'].median().__round__(1))

print('Percent not smoking:',
      (df2[df2['cigs'] == 0].shape[0] / df2.shape[0] * 100).__round__(1))

# 85% of women dont smoke thats why mean is inaccurate here

Mean cigs: 2.1
Median cigs: 0.0
Percent not smoking: 84.7

(iii) Among women who smoked during pregnancy, what is the average number of cigarettes

print("Average cigs among smokers:",
      df2[df2["cigs"] != 0]['cigs'].mean().__round__(1))

Average cigs among smokers: 13.7

(iv) Find the average of fatheduc in the sample. Why are only 1,192 observations used to compute this average?

print("Number Of Missing Data:", df2['fatheduc'].isna().sum())

print("Average father education:", df2['fatheduc'].mean().__round__(1))

Number Of Missing Data: 196
Average father education: 13.2

(v) Report the average family income and its standard deviation in dollars

print("Average family income", df2['faminc'].mean().__round__(1))

print("Standard deviation of family income", df2["faminc"].std().__round__(1))

Average family income 29.0
Standard deviation of family income 18.7

C3

The data in MEAP01 are for the state of Michigan in the year 2001. Use these data to answer the following questions.

df3 = dataWoo("MEAP01")
dataWoo('MEAP01', description=True)

name of dataset: meap01
no of variables: 11
no of observations: 1823

+----------+-----------------------------------------------+
| variable | label                                         |
+----------+-----------------------------------------------+
| dcode    | district code                                 |
| bcode    | building code                                 |
| math4    | % students satisfactory, 4th grade math       |
| read4    | % students satisfactory, 4th grade reading    |
| lunch    | % students eligible for free or reduced lunch |
| enroll   | school enrollment                             |
| expend   | total spending, $                             |
| exppp    | expenditures per pupil: expend/enroll         |
| lenroll  | log(enroll)                                   |
| lexpend  | log(expend)                                   |
| lexppp   | log(exppp)                                    |
+----------+-----------------------------------------------+

Michigan Department of Education, www.michigan.gov/mde

df3.head()

	dcode	bcode	math4	read4	lunch	enroll	expend	exppp	lenroll	lexpend	lexppp
0	1010.0	4937	83.300003	77.800003	40.599998	468	2747475.0	5870.672852	6.148468	14.826193	8.677725
1	2070.0	597	90.300003	82.300003	27.100000	679	1505772.0	2217.631836	6.520621	14.224816	7.704195
2	2080.0	4860	61.900002	71.400002	41.750000	400	2121871.0	5304.677734	5.991465	14.567809	8.576344
3	3010.0	790	85.699997	60.000000	12.750000	251	1211034.0	4824.836426	5.525453	14.006985	8.481532
4	3010.0	1403	77.300003	59.099998	17.080000	439	1913501.0	4358.771973	6.084499	14.464445	8.379946

(i) Find the largest and smallest values of math4. Does the range make sense? Explain.

print("max student satisfaction:", df3['math4'].max())

print("min student satisfaction:", df3['math4'].min())

max student satisfaction: 100.0
min student satisfaction: 0.0

df3.hist('math4', density=True)

array([[<Axes: title={'center': 'math4'}>]], dtype=object)

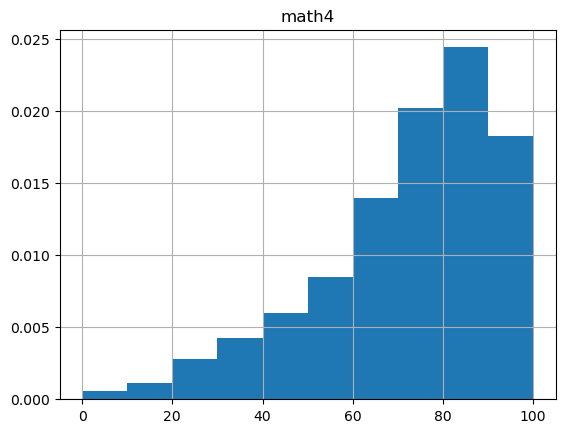
(ii) How many schools have a perfect pass rate on the math test? What percentage is this of the total sample?

print("schools with perfect math rate:", (df3['math4'] == 100).sum())
print("percentage of schools with perfect rate:",
      ((df3['math4'] == 100).sum() / df3.shape[0] * 100).__round__(1))

schools with perfect math rate: 38
percentage of schools with perfect rate: 2.1

(iii) How many schools have math pass rates of exactly 50%?

print("Number of schools with 50% passing rate:", (df3["math4"] == 50).sum())

Number of schools with 50% passing rate: 17

(iv) Compare the average pass rates for the math and reading scores. Which test is harder to pass?

print("Average math rate:", df3['math4'].mean().__round__(1))

print("Average reading rate:", df3['read4'].mean().__round__(1))
# reading seems to be harder in year 2001

Average math rate: 71.9
Average reading rate: 60.1

(v) Find the correlation between math4 and read4. What do you conclude?

df3.plot(x="math4", y="read4", kind='scatter')

<Axes: xlabel='math4', ylabel='read4'>

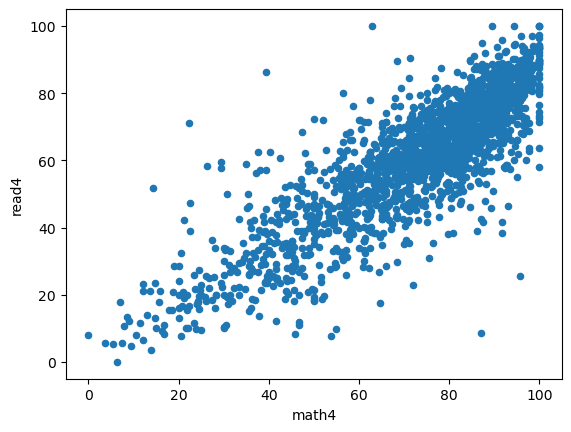
# correlation matrix
import numpy as np
np.corrcoef(df3["math4"], df3["read4"])

array([[1.        , 0.84272815],
       [0.84272815, 1.        ]])

print("correlation bet. math and read:",
      df3["math4"].corr(df3["read4"]).__round__(1))

correlation bet. math and read: 0.8

(vi) The variable exppp is expenditure per pupil. Find the average of exppp along with its standarddeviation. Would you say there is wide variation in per pupil spending?

(vii) Suppose School A spends 6,000 per student and School B spends 5,500 per student. By whatpercentage does School A’s spending exceed School B’s? Compare this to 100 · [log(6,000) –log(5,500)], which is the approximation percentage difference based on the difference in the natural logs.

C4

The data in JTRAIN2 come from a job training experiment conducted for low-income men during 1976–1977; see Lalonde (1986).

(i) Use the indicator variable train to determine the fraction of men receiving job training

(ii) The variable re78 is earnings from 1978, measured in thousands of 1982 dollars. Find the averages of re78 for the sample of men receiving job training and the sample not receiving job training. Is the difference economically large?

(iii) The variable unem78 is an indicator of whether a man is unemployed or not in 1978. What fraction of the men who received job training are unemployed? What about for men who did not receive job training? Comment on the difference.

(iv) From parts (ii) and (iii), does it appear that the job training program was effective? What would make our conclusions more convincing?